本宮小の日々

　３年生の図画工作科は現在、「未来にタイムスリップ」の活動に取り組んでいます。
　将来、自分がなりたい職業の絵を想像して絵に表現する活動です。
　今日12月6日(火)の３・4校時、3組の子どもたちが、夢をかなえた瞬間を思い浮かべながら、友だちと協力して夢や願いを絵にしていました。
　さて、どんな作品が出来上がるのでしょうか。楽しみです。

　１年生は、算数科「いろいろなかたち」の学習に入りました。
　今日12月5日(月)の2校時、1組の子どもたちが、家から持ってきた空き箱を積み重ねていろいろな形を作りました。（たくさんの様々な形の空き箱をあつめていただき、ありがとうございました。）
　どの向き、どんな形、どんな大きさの物が積み重ねやすいか、グループで考えて積んでいきます。

「これは、こうすると（縦にすると）高くなるよ。」
「大きいのを下にした方が、くずれないよ。」
「ぼくのお腹のあたりまで、届くように積もう！」

　箱の形、サイコロの形、筒の形などいろいろな形があるけど、工夫して上手に積むことができました。
　途中で失敗しても、その原因を考え、工夫しながら積み上げます。
　楽しみながら、かたちの学習ができましたね。

　２年生の生活科は現在、「うごくおもちゃをつくろう」の学習をしています。
　今日12月5日(月)の2校時、2組では、グループで決めたおもちゃづくりに取り組んでいました。

　協力し合い、アドバイスをし合いながら、「もっとよく動くおもちゃをつくろう！」と工夫しながら作っています。

　廊下には、材料もたくさん準備されていました。（身辺材の収集・提供にご協力いただき、ありがとうございます。）実際に、材料を目にすることで、発想に広がりが出てくるものです。

「こうした方が、転がるんじゃない。」
「もっと高く、飛ばしたいな。」
「スピードアップするには、〇〇したらいいよ。」

　より動くにはどうしたらよいか、子どもたちがあれこれ考え、試行錯誤しながら創意工夫を重ねていくさまは、とても微笑ましいものです。
　できあがったら、他のグループの友だちに作り方を説明し、一緒に遊ぶ機会が予定されているとのこと。
　楽しみですね。

　６年生の算数科は現在、「角柱と円柱の体積を求めよう」の学習に取り組んでいます。
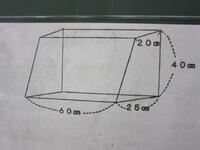
　今日12月３日(金)の2校時、２組では、下の写真のような立体の体積を求める学習に取り組みました。

　子どもたちはこれまで、「下の面」が底面で、その形は長方形や正方形、三角形といった「角柱」であったり、正円の「円柱」であったりする立体の体積を求める学習をしてきました。
　でも、今日の課題として示された立体は、「下の面」と「上の面」の形（大きさ）が異なります。
　これまでのように、「下の面」を底面と考えていたのでは、公式を使えない状況・・・さあ、どうする？　

　最初は「求められるかなぁ」「分からないなぁ。」と不安げな表情を浮かべていた子どもたちでしたが、「向きを変えて、これまで学習した形を手がかりにすれば、体積が求められそうだ！」という見通しをもとに、さっそく、グループになって課題解決に取組みはじめました。

　グループで話し合うときには、見通しが持てた子が中心となって、横向きにした用紙を手に持ち、
「これ（横向き）を、こうする（縦向き）と、ここの部分が台形でしょ。」
と、向きを変えながら、側面（台形）を底面と見る見方をグループの友だちに説明します。

「あ、そっか。台形！」
「底面積は、台形の面積と考えて・・・」
「じゃあ、公式は・・・」
「だとしたら、高さはここ？」
といった具合に、グループ全員が体積を導き出し、求める方を説明できるようになりました。

　またその後、全体で解決方法を発表し合う場面では、「図形を２つくっつけて大きな四角柱として考える方法」を導き出したグループもあって、その考え方を全体で共有することもできました。

　授業の振り返りでは、「〇〇くんが説明してくれたおかげで、向きを変えて台形と見れば体積を求められることがわかった。」といった記述があり、友だちの考えを次に生かそうとしている子どもがたくさんいました。

　いい学び方です。

　日々の授業の中、このような学習経験を繰り返すことで、子どもたちは、友だちと学ぶことのよさを感じ、協力しながら問題を解決していく資質や能力を鍛えています。

　3年生の算数科では現在、分数の大きさ比べやたし算、ひき算を学習しています。
　今日12月1日(木)2校時、3組の子どもたちが、分数の表し方と仕組みに着目し、同分母分数のたし算の仕方を考える授業に取り組みました。

　授業では、すでに学習している「小数のたし算は、０．１をもとにして考えた経験」を手がかりに、「今日は分数だから、1／10を手がかりにすればできそうだ！」と見通しを立て、問題「3／10＋2／10」の計算方法を考えました。

　見通しが立てた子どもたちは、さっそく、リットルますの図や数直線など、それぞれが選んだ方法を使って考えをノートにまとめ、自分の考えた計算の仕方を発表しあいました。

　分数のたし算は、「なぜそうなるのか」をきちんと説明できることが大切です。
　ペアや全体で話し合いをする場面では、リットルますの図に貼られたテープを操作しながら、
　「3／10は1／10の3つ分で、2／10は1／10の2つ分だから・・・」
　「1／10をもとにするから、３＋２で・・・」
と、自分が導き出した考えの根拠を明確にしながら説明したり、友だちの発表を聞いて気づいた根拠をつぶやいたりする子どもがたくさんいました。

　最後に、式やリットルますの図、数直線、いずれの方法でも「1／10をもとにすること」が共通点であることを導き出し、同じ分母どうしの分数のたし算の計算の仕方について、みんなで確認しながら文章にまとめることができました。
　振り返りの場面では、次時で扱う「ひき算も同じ考え方でできそう・・・」という感想を記入した子も！　いい学び方をしていますね。