五百川小の日々
5年:稲の観察 ~ たくさんの稲穂が実りますように ~
学校のベランダには、ペットボトル稲を栽培しています。
ペットボトル稲といっても、特殊な品種ではなく、以下の写真のように育てています。
<ペットボトル稲に関して、子どもたちの抱いた新たな疑問や感想>(一部抜粋)
・ 1本しか植えていないのに2本になっている?これからどうなるのだろう?
・ 下の方の根っこがうずまいていた?
・ 稲が10cm以上になっていてびっくりしました。このまますくすくと大きく育ってほしいと思います。
16日(木)。子どもたちは、後藤さんの家の田んぼに行ってきました。
<田んぼの稲に関して、子どもたちの抱いた新たな疑問や感想>(一部抜粋)
・花が開花していた。葉がとても分かれていた。作溝してあった。
・ペットボトル稲よりもすごく大きかった、葉の数が多かった。
・1つでどんぐらいできるのかな?
・ぼくのペットボトルの苗ももっと大きくなってほしい。
・タニシやアメリカザリガニもいた。肥料がまいてあった。
新たな疑問をもとに、友達と共に学びを深め合いながら、ペットボトル稲と田んぼの稲の双方に、たくさんの稲穂が実るよう、これからも栽培と観察を続けていきたいと思います。
御稲プライマルの後藤さんの常日頃のご協力に、改めて、心より感謝申し上げます。
主体的・対話的で深い学びを目指して
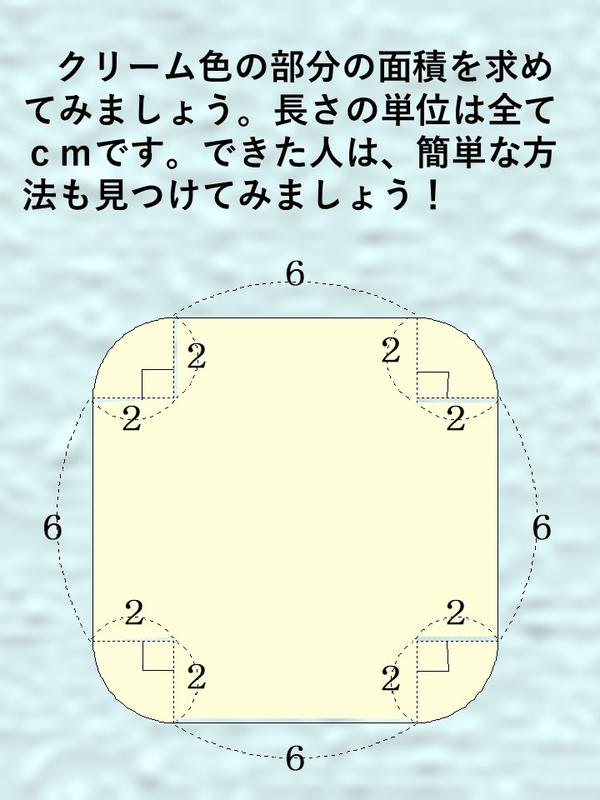
算数寺子屋 ~簡単な面積の求め方を見つけよう!~
七夕集会
本日は七夕集会がありました。とは言え、今年度は例年のような集会を実施することができなかったので、各学級で七夕の企画を立てて実施しました。
先生からの七夕についての話を熱心に、そして楽しそうに聞く姿、友だちの願い事を興味深く聞く姿は、五百川っ子らしい素晴らしい姿だと感じました。
今年も将来の夢など、様々願い事が聞かれました。特に今年度は、新型コロナウイルスによる臨時休業を経験したこともあり、家族の健康や幸せ、友だちの幸せを願う願い事が多く聞かれました。「じいじ、ばあばが元気でいられますように」「お父さん、お母さん、妹が健康でいられますように」「みんなが幸せでありますように」そのような思いやりあふれる願い事に、心が温かくなりました。6年生は今年度が最後ということもあり「いつまでも友だちと仲良くいられますように」「このクラスが最高のクラスになりますように」などの願い事も聞かれました。
素直な子どもたちの願い事が叶うよう、これからも子どもたちを応援していきたいと思います。
大輪の花咲け! ~ produced by ひまわり会 ~
続~花には水やりを・・・人には思いやりを!
ゲーム開発者になってみよう!
「プログラミング教育授業実践」
今年度から本格的にプログラミング教育が始まりました。昨年度の学習の成果を生かしながら、6年生は「ゲーム開発者になってみよう」という単元で、2年生のためにかけ算の練習をするゲームづくりに取り組みました。
「問題に正解したときは、こんな音を流したい」
「問題がだんだん難しくなるようにするには?」
「ゲームをクリアしたらこんな言葉でほめてあげたい」
「ゲームをクリアできなかった時は、こんな言葉で励ましてあげたい。」
子どもたちは、2年生が喜んでくれるようなゲームをつくろうと、試行錯誤しながら一生懸命に取り組んでいました。
授業の最後には、友だちのつくったゲームをみんなで見ながら、それぞれのアイディアに感心し合う姿が見られました。
4年:人権教育 ~ まずは、担任からはじめよう ~
花には水やりを人には思いやりを!!
※ 安全のため、ソーシャルディスタンスをとりながら撮影を行いました。多少のゆれはご了承ください。スマホを横向きにしていただくと、より大きい画面でご覧いただけます。
5・6年合同:花壇に花の苗を植えました!
3年:〇〇の苗を植えました!
校章~ school emblem ~
子どもたちへのエール~Stick to it ! Stay strong.~
気を引き締め、一歩前進!
安心・安全・免疫力向上計画
学校再開です!
25日(月)学校再開いたしました。
学校では、引き続き、感染防止の対策に努めてまいりますので、ご家庭におかれましても、「気をつけよう」からはじめよう!の継続をよろしくお願いいたします。
感染予防への取り組み~学校給食編~
再生時にエラーが出る場合は、再試行をお願いします。
学校の再開について
webにもアップいたしました。ご活用ください。
(メール文と内容は同じです!)
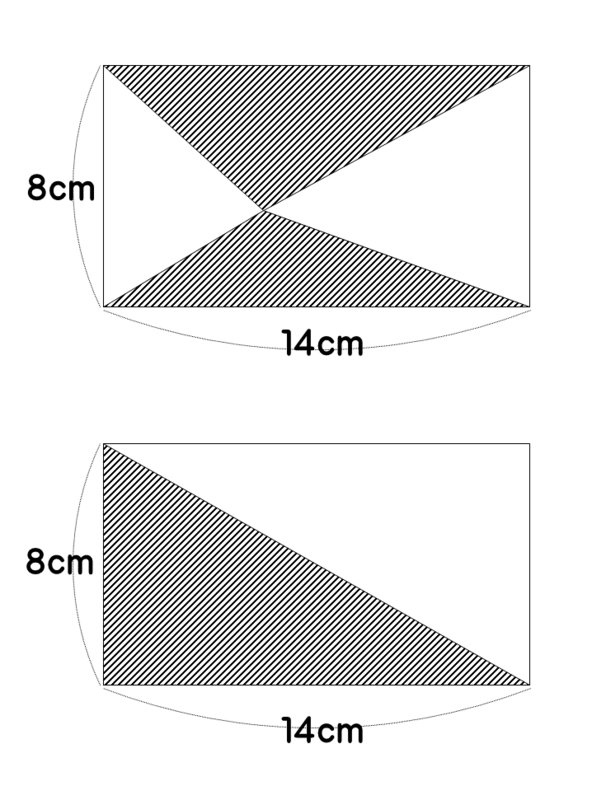
どちらが広いかな?それとも・・・?
広さ(面積)の問題です。ただし、ここに描かれている2つの四角形は長方形です。
上の図形(三角形2つ分)と下の図形(三角形1つ分)とでは、どちらの面積(斜線部分)が広いと思いますか?Let's try.
ヒント:上の図形で、2つの三角形のおのおのの高さを適当に決めて考えると、わかるかも!
※ 中学校の数学レベルになりますが、たとえば、上の図で底辺をa、おのおのの高さをb1、b2、下の図で底辺をa、高さをbと決めて考えると、底辺や高さがどんな長さでも同じ結果になることがわかります。